微分の本質とは?!なんとなく解いてる人必見!
こんにちは!
授業をしない塾、武田塾三軒茶屋校です。
今回のテーマは「微分」について
微分の式変形は覚えたけど何のために何をやってるのかわからない…
特に数Ⅲではなく、数ⅡBまでしか使わないひとに多いと思います。
そんな人のためにわかりやすく微分の本質について触れていきたいと思います!
◆そもそも微分ってなんでできた?
微分積分はニュートンとライプニッツという人物が違う国でほぼ同時期に作りました。
ニュートンはみなさんご存知だと思います!
ニュートンと言えば、リンゴが木から落ちていくところから「万有引力の法則」を考えたことで有名ですね!!
ではそのニュートンがなぜ微分を考えたのでしょうか?
それは物理を考えていくうえで必要になったからだといわれています。
例えば次のような問題を考えてみて下さい。
【問題】
ある車が一定の速さvで走っていたところ、2時間で4km進みました。このときの速さvを求めなさい。
物理を習っていない人でも中学生の「き・は・じ」を使えば求められますね!
「速さ=距離の変化量÷時間の変化量」で4km÷2時間=2km/hとなります。
実はこの速さを求めるような計算をするために微分が生まれたんです!!
どういうことか説明する前に、いったんグラフについておさらいしましょう!
◆v-tグラフ「傾き=速さ」
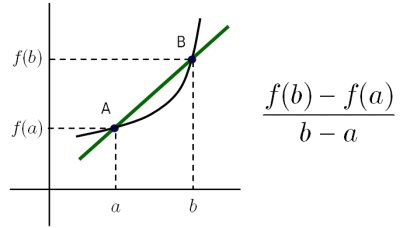
みなさん!一次関数のグラフ(直線)の傾きを計算するときどうやって計算していますか?
横軸をx、縦軸をyとすれば、「yの変化量÷xの変化量」で求められたと思います。
では横軸を時間、縦軸を距離としてみましょう。これをv-tグラフと言います。
このグラフの傾きは「距離の変化量÷時間の変化量」となりますね。
この式、先ほど見覚えがありませんか?
そうv-tグラフ(直線)の傾きは速さになるんです。
今回は一次関数の簡単なグラフで、速さが一定でした。
でも実際は速さが複雑に変化していますよね。
このときどのように計算すればいいのでしょうか??
◆複雑な速さを知りたい!→微分発生!!
一次関数なら傾きを求められるというのは今見てきました。
複雑なグラフも一次関数のように見る方法はないでしょうか.…?
その方法はズバリ「ズームする‼」です!
極端にズームすれば曲線もほぼ直線に見えるのは分かると思います。
この原理を傾きを求める方法に落とし込むと、扱うxの変化量とyの変化量をごくわずかにしてしまえばいい!ということです。
速さなら、ごく一瞬(時間の変化量)に進む距離(距離の変化量)によってそのときの速さを求めるんです!!
つまり
速さ = 進んだ距離 / かかった時間 (かかった時間→0)
と式で表せます。
「→0」というのは限りなく0に近づける、ごくわずかにするという意味です。
ここで微分の公式を思い出してみて下さい。
f'(a) = { f(a+h) - f(a) } / h (h→0)
速さの求め方を理解していれば難しいことはありません。
右辺の分母はかかった時間に対応する「yの変化量」で、分子が進んだ距離に対応する「xの変化量」といえます。
そしてそのxの変化量をわずかにしていけば傾きが求まるということなんです。
◆まとめ
微分は速さ、つまり傾きを求めるためにできました!
『無料受験相談』___________________
武田塾三軒茶屋校では随時無料の受験相談を行っております。 志望校選び、正しい勉強方法、偏差値を上げる方法、将来のこと、どんな内容でも個別に対応いたしております。
【武田塾三軒茶屋校 三軒茶屋の個別指導塾・予備校】 〒154-0004 東京都世田谷区太子堂2-14-3 アーバンリゾート三軒茶屋ビル 3F 東急田園都市線 三軒茶屋駅 北口B 徒歩1分 TEL:03-6805-4347 FAX:03-6805-4397 Mail:sangenjaya@takeda.tv
用賀駅から6分♪
桜新町駅から4分♪
お洒落な恵比寿からも近い♪
















